Introducing Elliptic Curve Cryptography (ECC)
Elliptic curve cryptography (ECC) is an encryption method that utilizes public keys and is grounded on the theory of elliptic curves. It facilitates the creation of cryptographic keys that are more efficient, faster, and smaller. Rather than employing the conventional approach of generating keys through the multiplication of large prime numbers, ECC leverages the properties inherent in the elliptic curve equation.
This technology is compatible with most public key encryption techniques, including RSA and Diffie-Hellman. Because Diffie-Hellman and RSA cryptographic methods are based on the creation of keys by using very large prime numbers. Hence, key creation requires a lot of computational power. According to some researchers, ECC can achieve the same level of security with a 164-bit key where other systems require a 1,024-bit key. Because ECC helps to establish equivalent security with lower computing power and battery resource usage, it is becoming widely used for mobile applications. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S. Miller in 1985 and elliptic curve cryptography algorithms entered wide use around 2004.

TLS Machine Identity Management for Dummies
RSA vs Elliptic Curve Cryptography: The need for a new cryptographic algorithm
The key characteristic of the RSA algorithm is that it contains one process that is easy to do but difficult to undo. The easy part of the algorithm multiplies two prime numbers, while the difficult pair is factoring the product of the multiplication into its two component primes. Algorithms that have this characteristic are known as Trapdoor Functions. Finding a good Trapdoor Function is critical to making a secure public key cryptographic system. Simply talking, the bigger the spread between the difficulty of going one direction in a Trapdoor Function and going the other, the more secure a cryptographic system based on it will be.
The problem of factoring has a long history of study, dating back to ancient methods such as the Sieve of Eratosthenes used to determine all prime numbers up to a specified limit. However, as mathematics and computational capabilities have evolved, the gap between the complexities of factoring large numbers and multiplying them has been diminishing. This necessitates the keys to grow at an even more rapid pace. This is not a feasible scenario for mobile and low-power devices with restricted computational capabilities. The disparity between factoring and multiplication is not viable in the long run. This indicates that the RSA system may not be the optimal choice for the future of cryptography. In fact, recent studies have shown that RSA keys, even those as long as 2048-bits, can be effectively compromised through either man-in-the-browser or padding oracle attacks. To go a step further, the study recommends that the most effective solution is to phase out the RSA key exchange and transition to elliptic curve cryptography.
What is an elliptic curve, and how does it relate to cryptography?
But what exactly is an elliptic curve and how does the underlying Trapdoor Function work? In the context of elliptic curve cryptography (ECC), an elliptic curve is a mathematical structure used to define a set of points that satisfy a specific equation of the form y2=x3+ax+by^2 = x^3 + ax + by2=x3+ax+b over a finite field. These points, along with a defined operation (point addition), form the basis of ECC algorithms, which rely on the computational difficulty of the elliptic curve discrete logarithm problem (ECDLP) for security. In cryptography, elliptic curves are used to generate smaller, faster, and more efficient keys compared to traditional algorithms like RSA, while providing equivalent levels of security. This efficiency makes ECC particularly well-suited for environments with limited computational resources, such as mobile devices and IoT, where performance and low power consumption are critical.
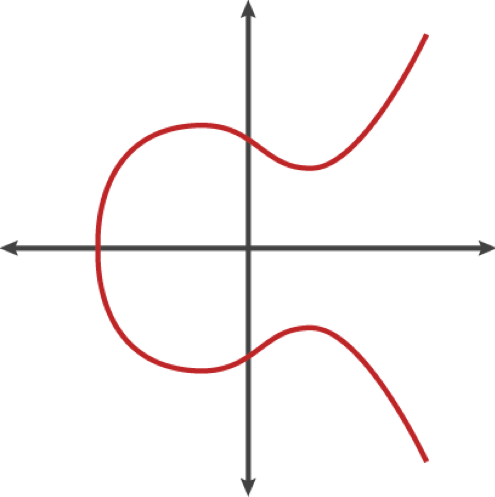
Picture 1: Elliptic curve (source: blog.cloudflare.com)
Multiplying a point on an elliptic curve by a specific number generates another point on the curve. However, determining the number used in this operation is extremely challenging, even if you have knowledge of the initial point and the outcome. This feature of elliptic curve-based equations is crucial for cryptography because while they are relatively simple to carry out, reversing them is exceedingly hard.
The tough challenge at the heart of elliptic curve cryptography is the elliptic curve discrete logarithm. Despite nearly 30 years of study, no algorithm has been discovered that can solve this problem more efficiently than the most straightforward method. Unlike factoring, no shortcuts appear to exist that can close the gap in a Trapdoor Function centered on this problem, based on our current understanding of mathematics. This implies that for numbers of equal size, the task of solving elliptic curve discrete logarithms is considerably more difficult than factoring. Given that a more computationally demanding problem results in a stronger cryptographic system, it is logical to conclude that elliptic curve cryptosystems are tougher to crack than RSA and Diffie-Hellman.
To illustrate the difficulty of breaking elliptic curve cryptography, Lenstra, Kleinjung, and Thome introduced the idea of "Global Security" in 2013. This concept allows you to calculate the energy required to crack a cryptographic algorithm and compare it to the amount of water that energy could heat to boiling point. This comparison can be thought of as a cryptographic carbon footprint. According to this measure, cracking a 228-bit RSA key uses less energy than boiling a teaspoon of water. On the other hand, breaking a 228-bit elliptic curve key would require enough energy to boil all the water on the planet. Achieving this level of security with RSA would necessitate a key that is 2,380-bits long.
Elliptic curve cryptography allows for the use of smaller keys while maintaining the same level of security. This feature is particularly useful in an era where more cryptography is being performed on less powerful devices such as mobile phones. While multiplying two prime numbers is simpler than breaking down the product into its constituent parts, the multiplication process can become time-consuming on a low-power device when the prime numbers become extremely large. Although increasing the key length could potentially maintain the security of RSA, this would result in slower cryptographic performance on the client's end. Elliptic curve cryptography seems to offer a superior compromise: high security with short, efficient keys.
Although there are certain cautions when implementing elliptic curve cryptography, such as the use of a good source of random numbers on the machine making the signatures, the advantages of elliptic curve cryptography over traditional RSA are widely accepted.
Common Use Cases for Elliptic Curve Cryptography
Elliptic curve cryptography is now used in a variety of applications: the U.S. government uses it to protect internal communications, the Tor project uses it to help assure anonymity, it is the mechanism used to prove ownership of bitcoins, it provides signatures in Apple's iMessage service, it is used to encrypt DNS information with DNSCurve, and it is the preferred method for authentication for secure web browsing over SSL/TLS. Here are some common use cases for elliptic curve cryptography (ECC):
- Secure key exchange
ECC is often used in key exchange protocols, such as the Elliptic Curve Diffie-Hellman (ECDH) key exchange. This allows two parties to securely exchange cryptographic keys over an insecure channel, which can then be used for subsequent symmetric encryption of communication. - One-way encryption for emails and data
ECC can be employed for one-way encryption, ensuring that data and emails are protected during transmission or storage. This is commonly done using algorithms like Elliptic Curve Integrated Encryption Scheme (ECIES), where small key sizes are ideal for scenarios where bandwidth and storage are limited. - SSL/TLS for secure web communication
ECC is increasingly being used in the context of SSL/TLS for securing web communication. Modern web browsers and servers support ECC-based cipher suites, providing a more efficient and secure alternative to traditional algorithms. - Internet of Things (IoT) device security
The resource efficiency of ECC makes it suitable for securing communication in IoT devices, which often have limited computational power, memory, and battery life. ECC enables secure communication between IoT devices and ensures the confidentiality and integrity of data. - Smart cards and embedded systems
ECC is commonly implemented in smart cards and embedded systems due to its efficiency in terms of key size and computational requirements. This is particularly important in scenarios where hardware resources are constrained. - Mobile device security
ECC is well-suited for mobile device security, where computational resources, battery life, and bandwidth are critical considerations. Its efficiency makes it a preferred choice for securing communications and data on mobile platforms. - Digital signatures in cryptocurrencies
ECC is extensively used for creating digital signatures in cryptocurrencies like Bitcoin and Ethereum. Digital signatures play a crucial role in ensuring the integrity and authenticity of transactions. The efficiency of ECC allows for smaller key sizes compared to RSA, making it more suitable for the resource constraints of blockchain networks. This results in faster transaction processing and reduced computational overhead.
Conclusion
Many specialists are expressing concern that the mathematical algorithms underpinning RSA and Diffie-Hellman may be compromised within the next 5 years. Indeed, the advancements in quantum computing are expected to provide computational abilities that will enable us to tackle mathematical challenges, such as factoring extremely large prime numbers, which were previously deemed unsolvable. The potential of quantum computing to process an enormous amount of data at an incredible speed is paving the way for revolutionary possibilities in several scientific fields, including data protection methodologies. One aspect of data protection that will be impacted by the capabilities of quantum computing is encryption, as existing encryption algorithms will become outdated, given they could be decoded in significantly less time.
(This post has been updated. It was originally published on January 4, 2019.)
